Пан Атаман Идеал САПРический. Часть 4. Гео Мутьрия. Тема 2

В прошлый раз, была затронута классификация подходов к описанию трехмерной геометрии, но ей и ограничились. Сегодня в сжатом виде рассмотрим три первых подхода – твердотельный, поверхностный и каркасный.

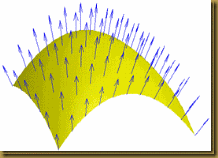
  Итак, подходы твердотельного моделирования служат для описания объемной сплошной геометрии. O(x,y,z), X_O(u,v,w), Y_O(u,v,w), Z_O(u,v,w). Объем описывается с помощью внешних граней (граничных поверхностей), грани состоят из куска поверхности и граничного контура, контур состоит из набора ребер, а ребра это кусок линии (не всегда прямолинейной) ограниченной двумя вершинами, вершины это точки в пространстве. Функция O выдает 1 если мы находимся внутри объема или на его границе, и ноль если мы находимся вне заданного объема. Нормали граней всегда направлены наружу тела.

Как говорилось в старых анекдотах, если вы хотите смоделировать пористое тело типа головки сыра – оно все равно у вас получится твердотельным и сплошным.

 Поверхностное моделирование служит для описания объектов, для которых одним из измерений (толщина) можно пренебречь по каким либо причинам. . S(x,y,z) X_S(u,v), Y_S(u,v), Z_S(u,v). В общем случае геометрия создаваемых поверхностей конечна, базируется на уравнении условно «бесконечной» поверхности и на ограниченном контуре. Контур состоит из граничных линий и вершин. Почему-то когда говорят про края поверхности, то граничные линии обычно не называют ребрами. Поверхность имеет такое понятие как направление нормали, и две стороны – положительную и отрицательную (внешнюю и изнаночную)

 

Каркас описывает не столько геометрию, сколько взаимосвязи элементов (точек и вершин) с помощью линейных и криволинейных отрезков. W(x,y,z) X_F(u), Y_F(u), Z_F(u). Содрежит информацию о координатах вершин и их соединении друг с другом

Впрочем, было бы все так просто, не было бы стольких книг и математических изысканий, позволяющих лучшим образом использовать эти подходы. Но прежде чем дальше углубляться, необходимо аналогичным телеграфным стилем описать оставшиеся подходы. Что и будет сделано в самом ближайшем будущем.